Trials of an Intel Quad Processor System: 4x E5-4650L from SuperMicro
by Ian Cutress on July 3, 2013 10:00 AM EST- Posted in
- CPUs
- Workstation
- Supermicro
- 4P
- Compute

Trials of an Intel Quad Processor System: 4x E5-4650L from SuperMicro
In recent months at AnandTech we have tackled a few issues of dual processor systems for regular use, and whether having a dual processor system as a theoretical scientist may help or hinder various benchmark scenarios. For the problems that I encountered as a theoretical physical chemist, using a dual processor system without any form of formal training dealing with memory allocation (NUMA) resulted in a severe performance hit for anything that required a significant level of memory accesses, especially grid solvers that required pulling information from large arrays held in memory. Part of the issue was latency access dealing with data that was in the memory of the other CPU, and thus a formal training in writing NUMA code would be applicable for multi-processor systems. Nevertheless in my AnandTech testing we did see significant speedup when dealing with various ‘pre-built’ software scenarios such as video conversion using Xilisoft Video Converter, rendering using PovRay and our 3D Particle Movement Benchmark.
To take this testing one stage further, SuperMicro kindly agreed to loan me remote desktop access to one of their internal quad processor (4P) systems. The movement from 2P to 4P is almost strictly in the realms of business investment, except for a few Folding@home enthusiasts that have seen large gains moving to a quad processor AMD system using obscure buyers for motherboards and eBay for processors. But with 4P in the business realm, the software has to match that usage scenario and scale appropriately.
Our testing scenario will cover our server motherboard CPU tests only – as I only had remote desktop access I was not fortunate enough to do any ‘gaming’ tests, although our gaming CPU article may have shown that unless you are doing a massive multi-screen multi-GPU setup then anything more than a single Sandy Bridge-E system may be overkill.
Test Setup:
Supermicro X9QR7-TF+
4x Intel Xeon E5-4650L @ 2.6 GHz (3.1 GHz Turbo), 8 cores (16 threads) each
Kingston 128GB ECC DDR3-1600 C11
Windows Server Edition 2012 Standard
Issues Encountered
As you might imagine, moving from 1P to 2P and then to 4P without much experience in the field of multi-processor calculations was initially very daunting. The main issue moving to 4P was having an operating system that actually detected all the threads possible and then communicated that to software using the Windows APIs. In both Windows Server 2008 R2 Standard and 2012 Standard, the system would detect all 64 threads in task manager, but only report 32 threads to software. This raises a number of issues when dealing with software that automatically detects the number of threads on a system and only issues that number. In this scenario the user would need to manually set the number of threads, but it all depends on the way the program was written. For example, our Xilisoft and 3DPM tests do an automatic thread detection but set the threads to what is detected, whereas PovRay spawns a large number of threads despite automatic detection. Cinebench as well detected half the threads automatically, but at least has an option to spawn a custom number of threads.
Point Calculations - 3D Movement Algorithm Test
The algorithms in 3DPM employ both uniform random number generation or normal distribution random number generation, and vary in various amounts of trigonometric operations, conditional statements, generation and rejection, fused operations, etc. The benchmark runs through six algorithms for a specified number of particles and steps, and calculates the speed of each algorithm, then sums them all for a final score. This is an example of a real world situation that a computational scientist may find themselves in, rather than a pure synthetic benchmark. The benchmark is also parallel between particles simulated, and we test the single thread performance as well as the multi-threaded performance.
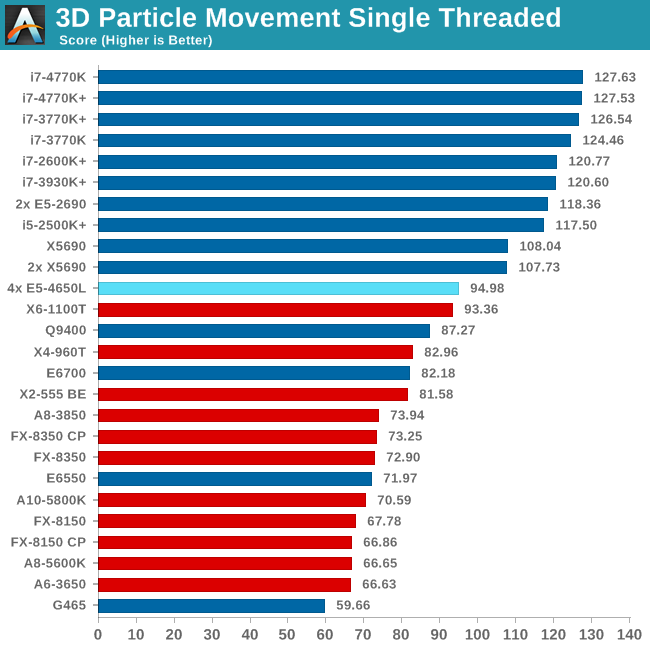
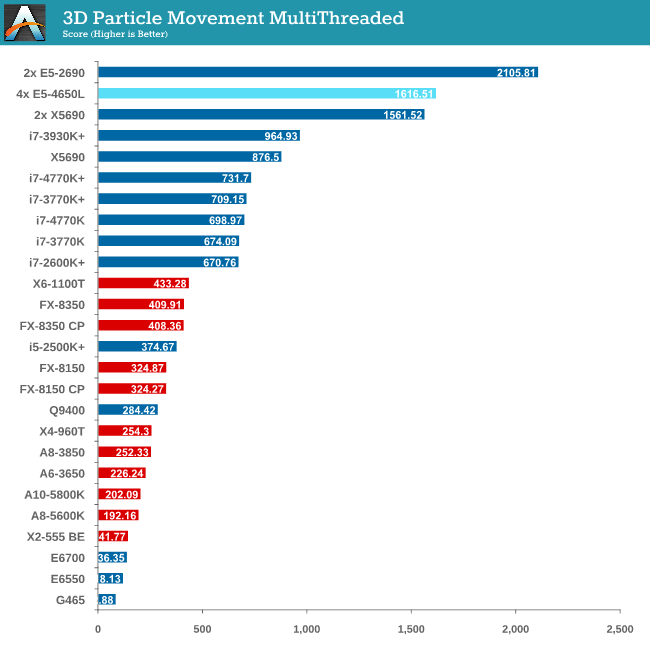
The 3DPM test falls under the half-thread detection issue, and as a result of the high threads but lower single core speed we only just get an improvement over a 2P Westmere-EP system. For single thread performance the single thread speed of the E5-4650L (3.1 GHz) is too low to compete with other Sandy Bridge and above processors.
Compression - WinRAR 4.2
With 64-bit WinRAR, we compress the set of files used in the USB speed tests. WinRAR x64 3.93 attempts to use multithreading when possible, and provides as a good test for when a system has variable threaded load. WinRAR 4.2 does this a lot better! If a system has multiple speeds to invoke at different loading, the switching between those speeds will determine how well the system will do.
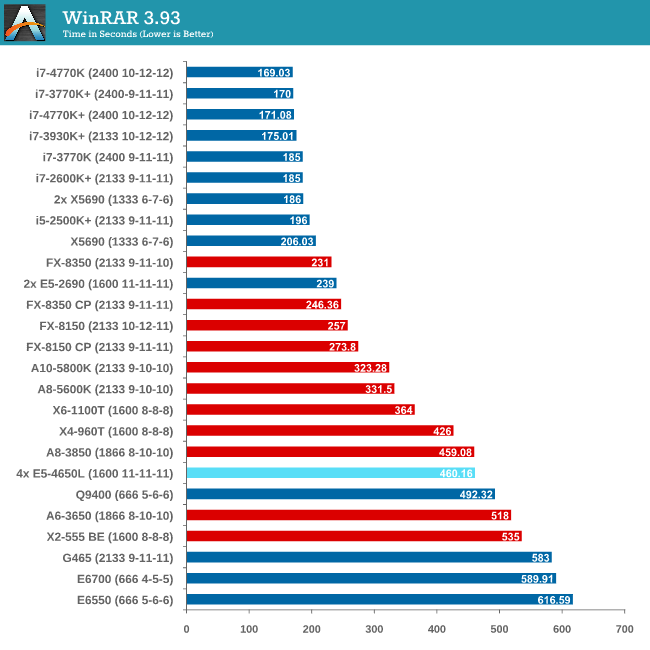
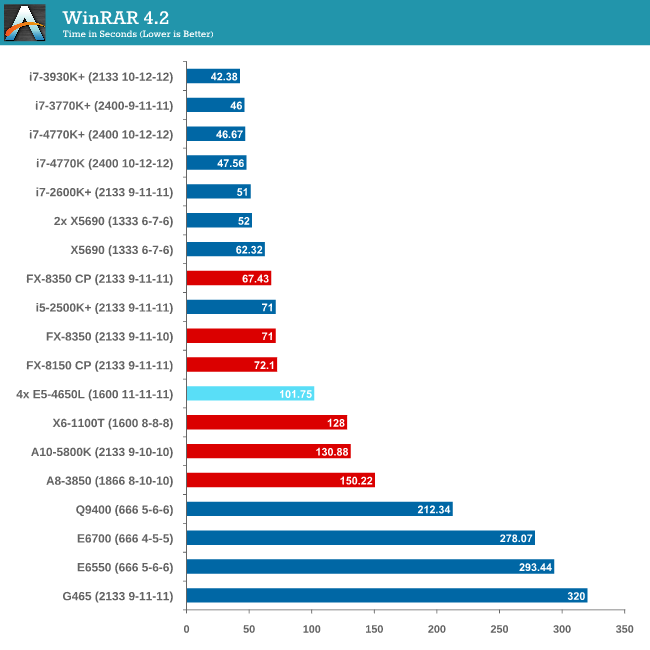
As WinRAR is ultimately dependent on memory speed, the 1600 C11 runs into the issues that the lower memory speed situations face. Despite this, the 2P Westmere-EP system still beats the 4P but you really need a good single core system with high bandwidth memory to take advantage.
Image Manipulation - FastStone Image Viewer 4.2
FastStone Image Viewer is a free piece of software I have been using for quite a few years now. It allows quick viewing of flat images, as well as resizing, changing color depth, adding simple text or simple filters. It also has a bulk image conversion tool, which we use here. The software currently operates only in single-thread mode, which should change in later versions of the software. For this test, we convert a series of 170 files, of various resolutions, dimensions and types (of a total size of 163MB), all to the .gif format of 640x480 dimensions.
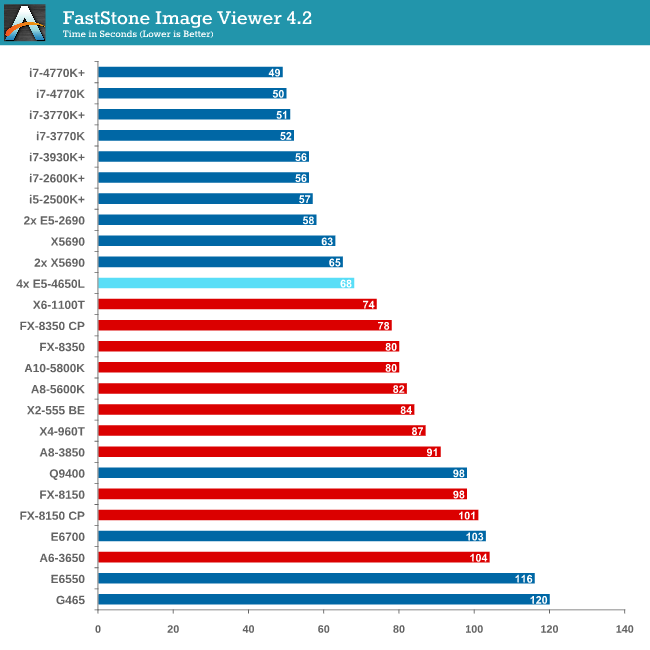
MHz and IPC wins for FastStone, which the single thread speed of the E5-4650Ls do not have.
Video Conversion - Xilisoft Video Converter 7
With XVC, users can convert any type of normal video to any compatible format for smartphones, tablets and other devices. By default, it uses all available threads on the system, and in the presence of appropriate graphics cards, can utilize CUDA for NVIDIA GPUs as well as AMD WinAPP for AMD GPUs. For this test, we use a set of 33 HD videos, each lasting 30 seconds, and convert them from 1080p to an iPod H.264 video format using just the CPU. The time taken to convert these videos gives us our result.
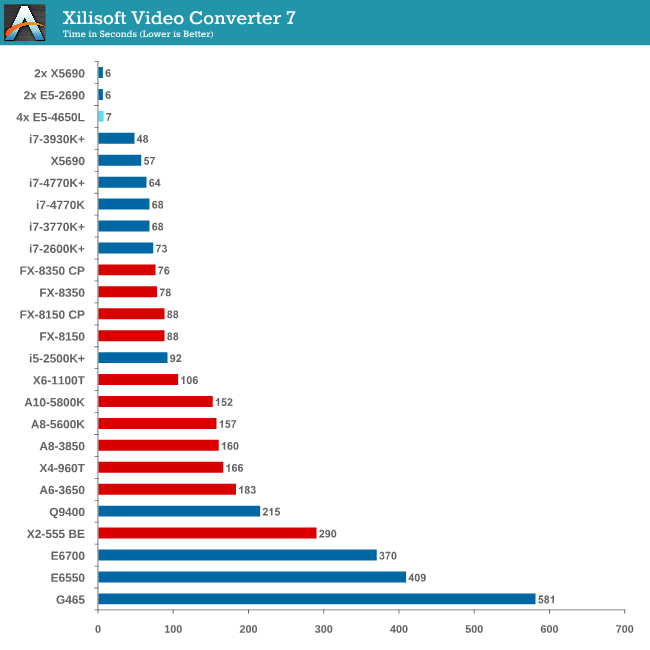
Due to the nature of XVC we do not see any speed up against Westmere-EP due to the 33rd video only being assigned a single thread, essentially doubling the time of the conversion.
Rendering – PovRay 3.7
The Persistence of Vision RayTracer, or PovRay, is a freeware package for as the name suggests, ray tracing. It is a pure renderer, rather than modeling software, but the latest beta version contains a handy benchmark for stressing all processing threads on a platform. We have been using this test in motherboard reviews to test memory stability at various CPU speeds to good effect – if it passes the test, the IMC in the CPU is stable for a given CPU speed. As a CPU test, it runs for approximately 2-3 minutes on high end platforms.
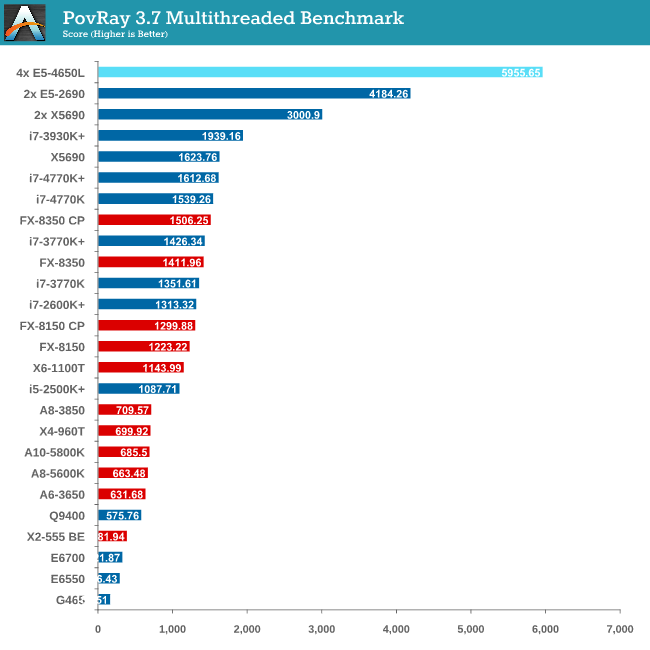
PovRay is the first benchmark that shows the full strength of 64 Intel threads, scoring almost double that of the 24 thread Westmere-EP system (which was at higher frequency).
Video Conversion - x264 HD Benchmark
The x264 HD Benchmark uses a common HD encoding tool to process an HD MPEG2 source at 1280x720 at 3963 Kbps. This test represents a standardized result which can be compared across other reviews, and is dependent on both CPU power and memory speed. The benchmark performs a 2-pass encode, and the results shown are the average of each pass performed four times.
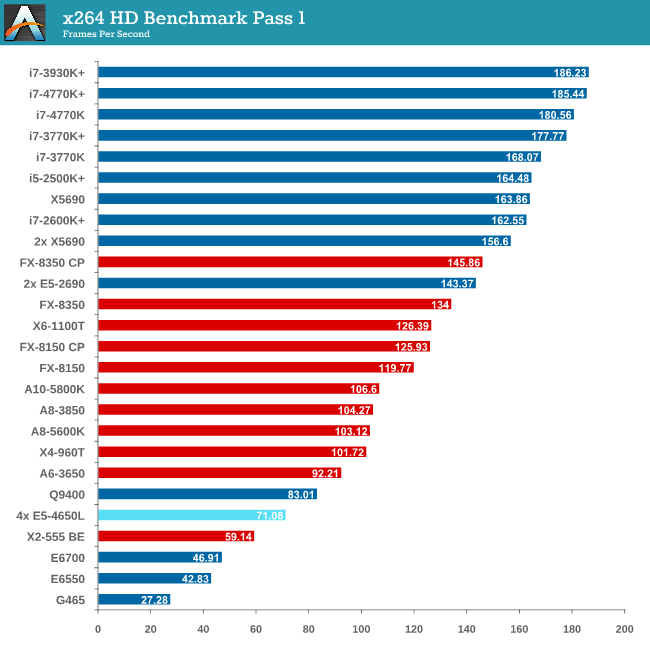
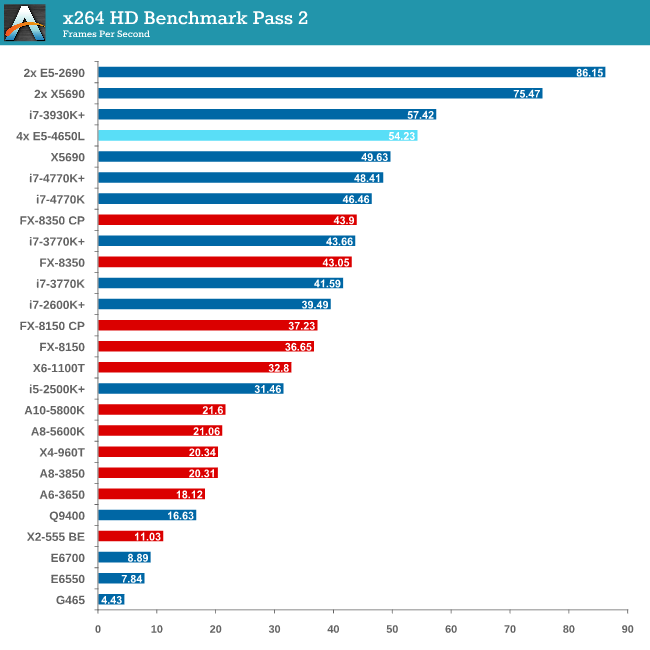
The issue with memory management and NUMA comes into effect with x264, and the complex memory accesses required over the QPI links put a dent in performance.
Grid Solvers - Explicit Finite Difference
For any grid of regular nodes, the simplest way to calculate the next time step is to use the values of those around it. This makes for easy mathematics and parallel simulation, as each node calculated is only dependent on the previous time step, not the nodes around it on the current calculated time step. By choosing a regular grid, we reduce the levels of memory access required for irregular grids. We test both 2D and 3D explicit finite difference simulations with 2n nodes in each dimension, using OpenMP as the threading operator in single precision. The grid is isotropic and the boundary conditions are sinks. Values are floating point, with memory cache sizes and speeds playing a part in the overall score.
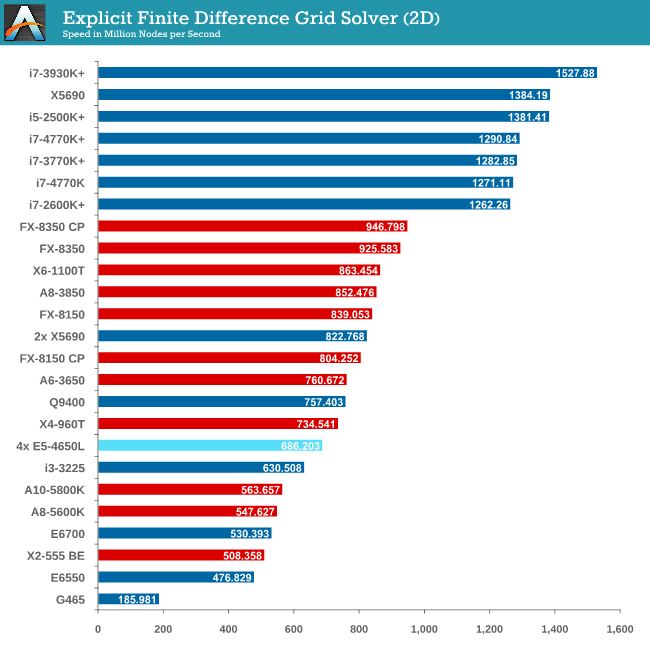
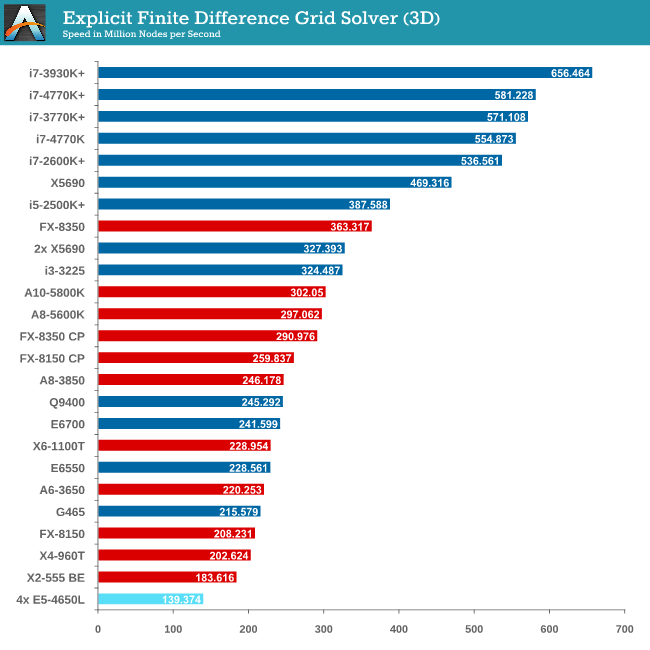
It seems odd to consider that a 4P system might be detrimental to a computationally intensive benchmark, but it all boils down to learning how to code for the system you are simulating. Porting code written for a single CPU system onto a multiprocessor workstation is not a simple matter of copy-paste-done.
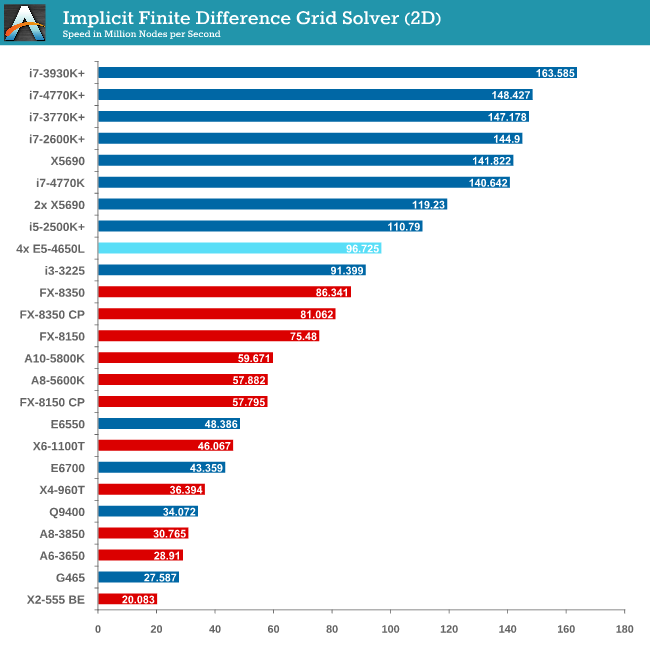
Grid Solvers - Implicit Finite Difference + Alternating Direction Implicit Method
The implicit method takes a different approach to the explicit method – instead of considering one unknown in the new time step to be calculated from known elements in the previous time step, we consider that an old point can influence several new points by way of simultaneous equations. This adds to the complexity of the simulation – the grid of nodes is solved as a series of rows and columns rather than points, reducing the parallel nature of the simulation by a dimension and drastically increasing the memory requirements of each thread. The upside, as noted above, is the less stringent stability rules related to time steps and grid spacing. For this we simulate a 2D grid of 2n nodes in each dimension, using OpenMP in single precision. Again our grid is isotropic with the boundaries acting as sinks. Values are floating point, with memory cache sizes and speeds playing a part in the overall score.
Conclusions – Learn How To Code!
For users considering multiprocessor systems, consider your usage scenario. If your simulation contains highly independent elements and lightweight threads, then the obvious suggestion is to look at GPUs for your needs. For all other purposes it is a lot easier to consider single CPU systems but scaling may occur if we look at memory management.
This makes sense when compiling your own code – the issue gets a lot tougher when dealing with third-party software. Before spending on a large multiprocessor system, get details from the company that make your software (for which you or your institution may be paying a large amount in yearly licensing fees) about whether it is suitable for multiprocessor systems, and do not be satisfied with answers such as ‘I don’t see why not’.
With Crystalwell in the picture in the consumer space, it becomes a lot more complex when dealing with a large eDRAM/L4 cache in a multiprocessor system. The system will then need to manage the snooping protocols for larger amounts of memory, making the whole procedure a nightmare for the unfortunate team that might have to deal with it. Crystalwell makes sense in the server space for single processor systems, perhaps dealing with MPI in clusters, but it might take a while to see it in the multiprocessor world at least. Fingers crossed…!











53 Comments
View All Comments
patrickjchase - Thursday, July 4, 2013 - link
One additional question for Ian: You state that your finite-difference solvers use "2^n nodes in each direction".Does this mean that the data offsets along the major axis (or axes in the 3d case) are also integer multiples of a large power of 2^n? For example, if you have a grid implemented as a 2D array named 'foo', what is the offset in bytes from foo[0][0] to foo[1][0]?
If those offsets have a large power-of-2 factor, then that would lead to pathological cache behavior and would explain the results you're getting. Experienced developers know to pad such arrays along the minor axis or axes. For example, if I wanted to use a 1024 x 1024 array, I might allocate it as 1024 x 1056 instead. The purpose of the extra 32 elements along each row is to ensure that consecutive rows don't contend for the same cache line.
0ldman79 - Thursday, July 4, 2013 - link
Guys...He has access through Terminal Services.
Exactly how is he going to test video cards and install Linux, hmm?
Nice article, though I confess I will have to read it again after a good nights sleep.
dealcorn - Thursday, July 4, 2013 - link
Supermicro IPMI solutions are generally well regarded and support remote OS installs. I assumed prior familiarity drove OS selection for better or worse.loki1725 - Thursday, July 4, 2013 - link
Really interesting article. I've written several implementations of Finite Difference solvers, and used both COTS and Open Source solvers for parallel machines. I'm really surprised by the results, but I really agree with the conclusion, of you don't write your software appropriately you won't take advantage of the hardware at your disposal.I know it's outside the scope of this article, but I would be really interested to see a comparrison of this 4x processors machine to a 'cluster' of two dual core machines. Ideally it would be awesome to see 2 Sci Linux clusters, one with 4 2x Xeons systems, and 1 with 2 4x Xeon systems. Put the same amount of RAM / core in both rigs and run computational benchmarks. When it comes down to purchasing hardware for a large cluster, looking for the price and performance break point is important. I would imagine that having more threads per machine would be faster then having to run your data over Infiniband (or something like it).
mapesdhs - Thursday, July 4, 2013 - link
Ian, do you have any idea how your code or these tests might run on an SGI UV 20 or
2000, given they have a hardware MPI system and other features to aid with NUMA
systems? The UV 20 is a quad-socket blade with up to 1.5TB RAM, while the 2000
scales to 256 sockets and up to 64TB RAM. They both use the XEON E5-4600 series.
Maybe you could ask SGI if you could do a remote access test on one of their UVs?
Ian.
wishgranter - Saturday, July 6, 2013 - link
Hi All, a letely we do some test on our photogrametric sw, and we stumbled on performance issues with Win2012 Datacenter editionon our DualXeon setups, ( http://www.agisoft.ru/forum/index.php?topic=1330.0 ) in short in W2012 is something not OK with the performance of sw, if we do same test on Win7, or XP the same hw is much more faster, up to 70% ( Hyperthreading stuff ) . Could we do more indepht benchmark/problem solving article put together ?? this could help a lot of people in realworld app usage.....lyeoh - Saturday, July 6, 2013 - link
It's normally silly to use such systems for embarrassingly parallel problems. With those problems you should use multiple far cheaper computers and get more performance for the $$$.These sort of systems are for those "scale vertically" problems.
alpha754293 - Monday, July 8, 2013 - link
You know that there are commercial codes written in MPI available for you to test with as well. And there's a few free ones too.Although you are right though, the transition from 2P to 4P is not as simple and straightforward as the transition from 1P to 2P.
jamesgor13579 - Tuesday, July 9, 2013 - link
In the real world, any heavy threading and computing workload wouldn't be running on Windows. There is a reason that large supercomputers use Linux, its much better at handling large NUMA systems.kgbogdan - Thursday, July 11, 2013 - link
In the future can you please try Linux? I think Linux can do a far better job than Windows. MS Windows Server environment is not that suitable for such benchmarks. And usually for more than 4p Server you use Enterprise Ed not Standard. Sorry, this is just an advice not mandatory, but please try Linux