The NVIDIA Titan V Deep Learning Deep Dive: It's All About The Tensor Cores
by Nate Oh on July 3, 2018 10:15 AM ESTA Shallow Dive Into Tensor Cores
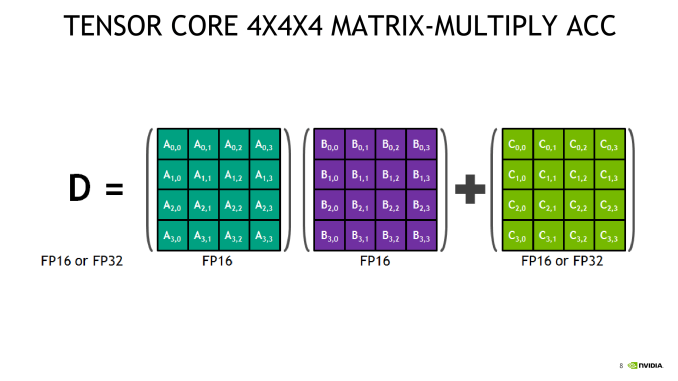
Of the several mysteries around Volta’s mixed precision tensor cores, one of the more nagging ones was the capability of 4 x 4 matrix multiplication. To recap, the tensor core is a new type of processing core that performs a type of specialized matrix math, suitable for deep learning and certain types of HPC. Tensor cores perform a fused multiply add, where two 4 x 4 FP16 matrices are multiplied and then the result added to a 4 x 4 FP16 or FP32 matrix. The result is a 4 x 4 FP16 or FP32 matrix; NVIDIA refers to tensor cores as performing mixed precision math, because the inputted matrices are in half precision but the product can be in full precision. As it so happens, the math that tensor cores do is commonly found in deep learning training and inferencing.
And if this sounds familiar to a normal GPU ALU pipeline, then it should. Tensor cores, while being brand-new to the GPU space, are not all that far removed from standard ALU pipelines. The density has changed – they're now operating on sizable matricies instead of SIMD-packed scalar values – but the math has not. At the end of the day there's a relatively straightforward tradeoff here between flexibility (tensor cores would be terrible at scalar operations) and throughput, as tensor cores can pack many more operations into the same die area since they are so rigid and require a fraction of the controlling logic when that cost is divided up per ALU.
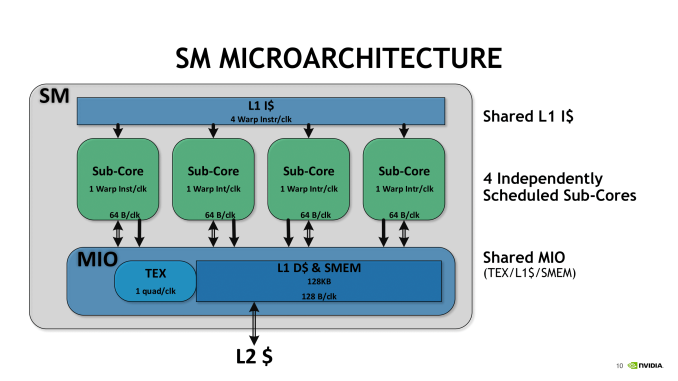
Consequently, while somewhat programmable, tensor cores are stuck to these types of 4 x 4 matrix multiplication-accumulation – and it’s not clear how and when the accumulation step occurs. Despite being described as doing 4 x 4 matrix math, in practice, tensor core operations always seem to be working with 16 x 16 matrices, with operations being handled across two tensor cores at a time. It appears that a lot of it has to do with the other changes in Volta, and more specifically, how these tensor cores are placed in an SM. For Volta, SMs were partitioned into four processing blocks, or sub-cores.
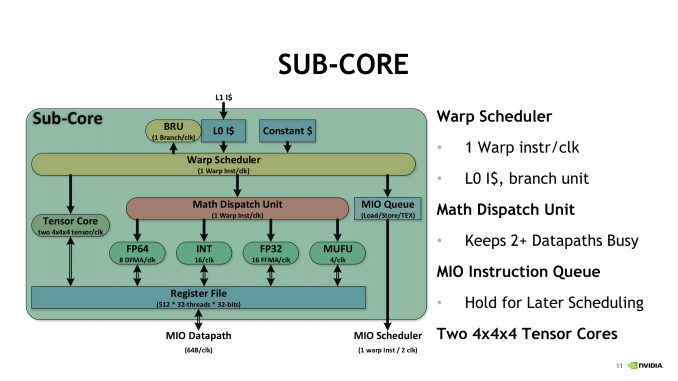
For each sub-core, the scheduler issues one warp instruction per clock to the local branch unit (BRU), the tensor core array, math dispatch unit, or shared MIO unit. For one, this precludes issuing a combination of tensor core operations and other math simultaneously. In utilizing the two tensor cores, the warp scheduler issues matrix multiply operations directly, and after receiving the input matrices from the register, perform 4 x 4 x 4 matrix multiplies. Once the full matrix multiply is completed, the tensor cores write the resulting matrix back into the register.
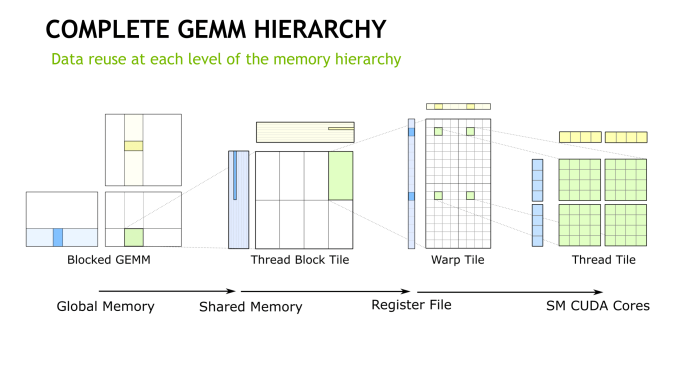
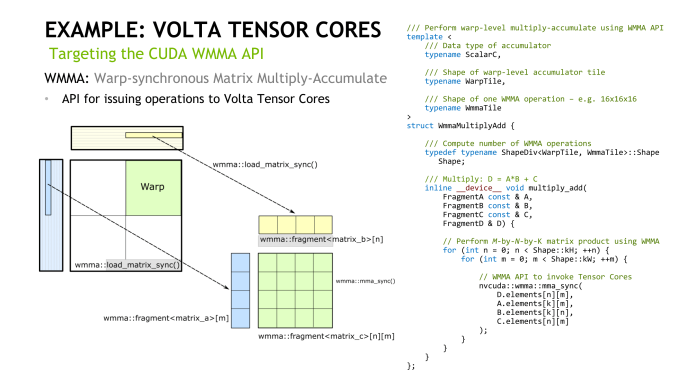
Looking at how tensor cores execute the actual instruction, opcode HMMA, only seems to raise more questions. Even at the compiler level with NVVM IR (LLVM), there are only intrinsics for warp-level matrix operations, rather than tensor cores, and warp-level remains the only level with CUDA C++ and the PTX ISA. Loading the input matrices is in the form of each warp thread holding a fragment, whose distribution and identity is unspecified. So broadly-speaking, it follows the same pattern of thread-level tiling-based GEMM computation for standard CUDA cores, and we'll circle back on that with NVIDIA's CUTLASS library in a moment.
In general terms, though, given the A*B+C tensor core operation, fragments consist of 8 FP16x2 elements (i.e. 16 FP16 elements) for A and another 8 FP16x2 elements for B, as well as 4 FP16x2 elements for an FP16 accumulator or 8 FP32 elements for an FP32 accumulator.
After the matrix multiply-accumulate operation, the result is spread out in fragments in the destination registers of each thread. Requiring warp-wide unity, these low-level operations essentially fail if one of the warp threads had exited.
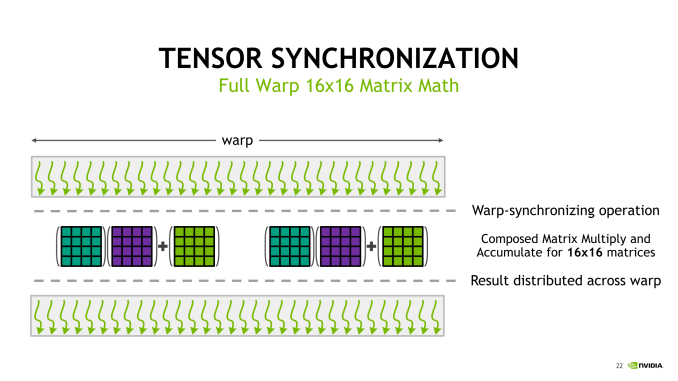
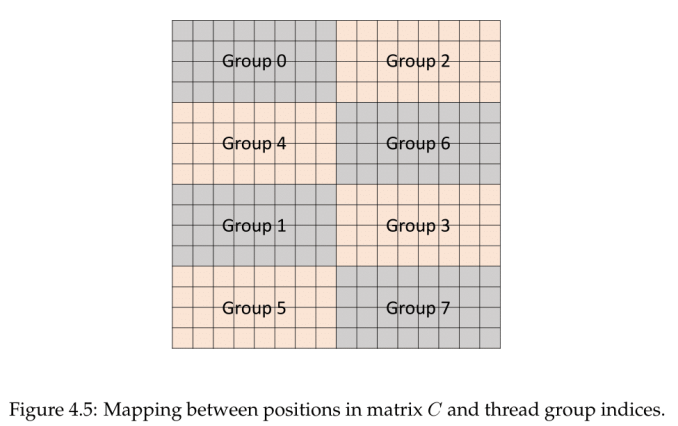
Low-level microbenchmarking by a team at Citadel LLC revealed a number of Volta microarchitecture details, including tensor core operations and the fragments involved, both locations in the register and identity compared to the input matrices. They observed that a sub-core proceeds to calculate the matrix-multiply in a particular patchwork pattern, with all 32 threads of the warp in action. Conceptually, the tensor cores operate on 4 x 4 submatrices to calculate the larger 16 x 16 matrix, involving Volta’s cooperative groups and new scheduling model.
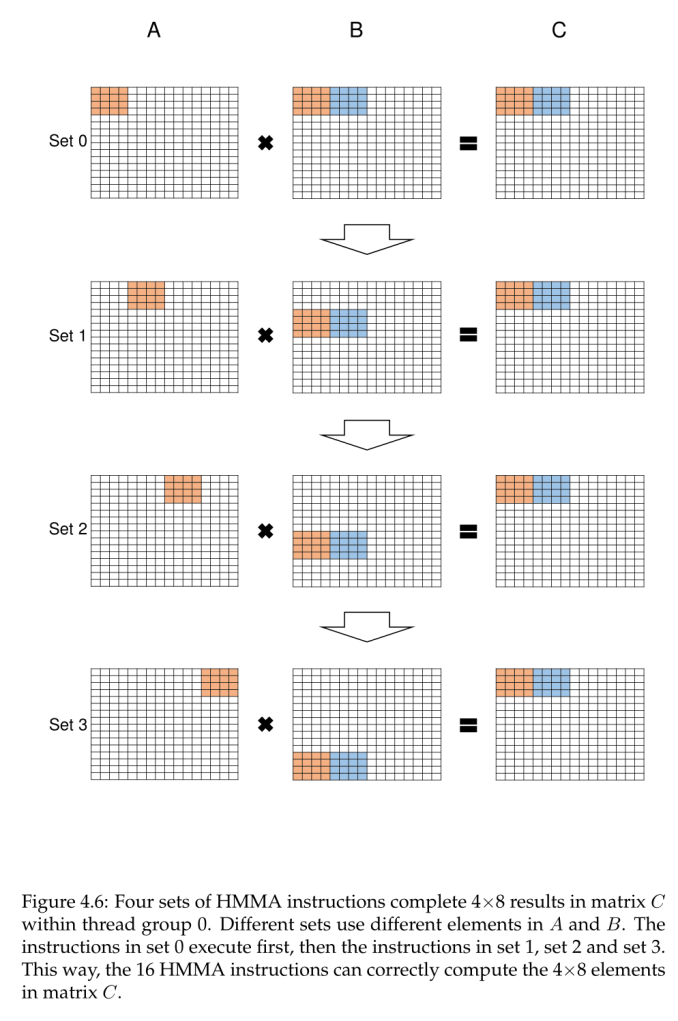
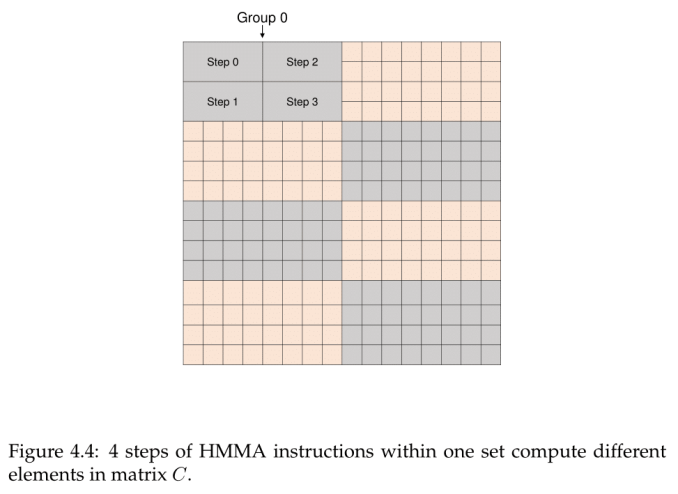
With the warp threads separated out into 8 thread groups of 4 threads, each thread group computed an 8x4 chunk serially, going through a process of 4 sets. So altogether, each thread group dealt with 1/8 of the resultant matrix.
Within a set were four HMMA steps that could be done in parallel, each applying to a 4x2 subchunk. The four threads were directly linked to those matrix values in the register, so that a single Step 0 HMMA instruction could be processed by the thread group to compute the subchunk in one go.
As matrix multiplication mathematically requires reuse of certain columns and rows, to permit parallel execution across all 8x4 chunk each 4 x 4 matrix is mapped to the registers of two threads. If applicable, the accumulate step sums the product with a stored accumulator; in this case of 4 x 4 submatrix operations to calculate a 16 x 16 parent matrix, this would include summing the sets as they were computed serially to form the corresponding chunk of 4 x 8 elements in the 16 x 16 matrix. Though untested by Citadel, it has been observed that FP16 HMMA instructions result in 2 steps rather than 4, relating to the smaller register space that FP16 occupies, and presumably a similar principle applies. Assuming that the sub-core was configured for peak output, it’s still hard to estimate without numbers, though it seems like ‘FMA ops per cycle’ is in reference to the matrices’ constituent values.
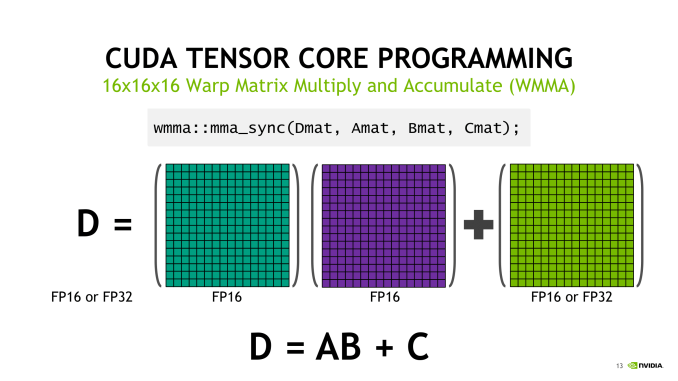
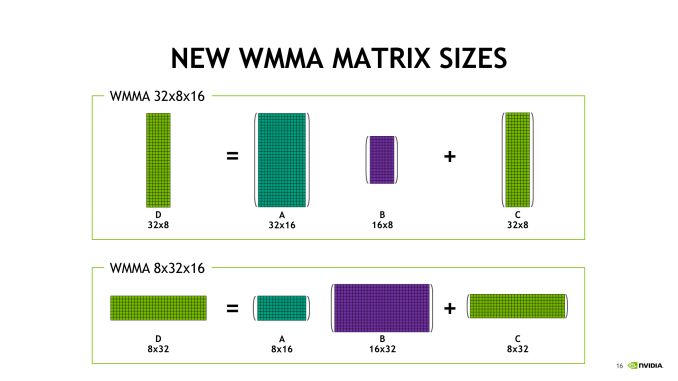
With independent thread scheduling and execution, as well as warp synchronization and warp-wide result distribution, the basic 4 x 4 x 4 tensor core operations translate into semi-programmable 16 x 16 x 16 mixed precision matrix multiply-accumulation, though with CUDA 9.1, 32 x 8 x 16 and 8 x 32 x 16 configurations are supported. For both new shapes, the multiplied matrices need the appropriate corresponding columns and rows of 16, with the end matrix being 32 x 8 or 8 x 32; this more-or-less suggests that standalone 4 x 4 x 4 matrix multiply-accumulate operations can’t be easily supported. Hard-coded warp-level behavior of register fragments, implementation of the MMA instruction, or tensor core ALUs could easily result in solely warp-level tensor core matrix math. And from a practical viewpoint, power consumption would suffer due to the increased register file usage while not significantly adding to deep learning performance.
How tensor cores operate seem to be a hardware implemented step of NVIDIA's GEMM computation hierarchy, as seen in CUTLASS, their CUDA C++ template library for GEMM operations. With traditional CUDA cores, the last step requires breaking down (i.e. 'decomposing') the warp tile structure into scalar and vector elements owned by individual threads. With the WMMA API, which right now means tensor cores, all that is abstracted away, leaving only the warp-cooperative matrix fragment load/store and multiply-accumulate to deal with. The accumulation occurs in-place as an FMA-type operation.
On the register level, NVIDIA themselves mentioned in their Hot Chips 2017 paper that “with three relatively small 4x4 matrices of multiply and accumulator data, 64 multiply-add operations can be performed.” And the per-thread program counter of the enhanced Volta SIMT model, something that enables tensor cores, usually requires 2 register slots per thread according to the whitepaper. There also may have been a change to the register structure; a 2-bank 64-bit configuration was reported by Citadel, though NVIDIA themselves have documented 4-bank 32-bit. The HMMA instructions themselves feature as much register reuse as possible, despite the other Volta enhancements (that we’ll touch on in a moment), so I can’t imagine registers aren’t bottlenecking tensor cores for the majority of cases.
For standalone 4 x 4 matrix multiply-accumulate, I suspect that the tensor core array was not physically designed for it in terms of registers, data paths, and scheduling, such that it is only useable with specific submatrix multiplications (though admittedly I’ve not studied linear algebra in some time).
In any case, from NVIDIA’s point-of-view, Volta isn’t a deep learning ASIC; it is still covering the GPGPU space, and so keeping to CUDA programmable tensor cores for applicability to GEMM/cuBLAS and HPC is only logical. With CUTLASS for CUDA C++, this is even more the case, as its WMMA API support is aimed at enabling tensor core GEMM operations for a broad range of applications. Fundamentally, the development of NVIDIA's deep learning hardware acceleration has much to do with the development of cuDNN (and cuBLAS, to a lesser extent) over the years.


-01_thumb.png)
-02_thumb.png)
-03_thumb.png)
-04_thumb.png)
-05_thumb.png)
-06_thumb.png)












65 Comments
View All Comments
Ryan Smith - Tuesday, July 3, 2018 - link
To clarify: SXM3 is the name of the socket used for the mezzanine form factor cards for servers. All Titan Vs are PCie.Drumsticks - Tuesday, July 3, 2018 - link
Nice review. Will anandtech be putting forth an effort to cover the ML hardware space in the future? AMD and Intel both seem to have plans here.The V100 and Titan V should have well over 100TF according to Nvidia in training and inference, if I remember correctly, but nothing I saw here got close in actuality. Were these benches not designed to hit those numbers, or are those numbers just too optimistic in most scenarios to occur?
Ryan Smith - Tuesday, July 3, 2018 - link
"The V100 and Titan V should have well over 100TF according to Nvidia in training and inference"The Titan V only has 75% of the memory bandwidth of the V100. So it's really hard to hit 100TF. Even in our Titan V preview where we ran a pure CUDA-based GEMM benchmark, we only hit 97 TFLOPS. Meanwhile real-world use cases are going to be lower still, as you can only achieve those kinds of high numbers in pure tensor core compute workloads.
https://www.anandtech.com/show/12170/nvidia-titan-...
Nate Oh - Tuesday, July 3, 2018 - link
To add on to Ryan's comment, 100+ TF is best-case (i.e. synthetic) performance based on peak FMA ops on individual matrix elements, which only comes about when everything perfectly qualifies for tensor core acceleration, no memory bottleneck by reusing tons of register data, etc.remedo - Tuesday, July 3, 2018 - link
Nate, I hope you could have included more TensorFlow/Keras specific benchmarks, given that the majority of deep learning researchers/developers are now using TensorFlow. Just compare the GitHub stats of TensorFlow vs. other frameworks. Therefore, I feel that this article missed some critical benchmarks in that regard. Still, this is a fascinating article, and thank you for your work. I understand that Anandtech is still new to deep learning benchmarks compared to your decades of experience in CPU/Gaming benchmark. If possible, please do a future update!Nate Oh - Tuesday, July 3, 2018 - link
Several TensorFlow benchmarks did not make the cut for today :) We were very much interested in using it, because amongst other things it offers global environmental variables to govern tensor core math, and integrates somewhat directly with TensorRT. However, we've been having issues finding and using one that does all the things we need it to do (and also offers different results than just pure throughput), and I've gone so far as trying to rebuild various models/implementations directly in Python (obviously to no avail, as I am ultimately not an ML developer).According to people smarter than me (i.e. Chintala, and I'm sure many others), if it's only utilizing standard cuDNN operations then frameworks should perform about the same; if there are significant differences, a la the inaugural version of Deep Learning Frameworks Comparison, it is because it is poorly optimized for TensorFlow or whatever given framework. From a purely GPU performance perspective, usage of different frameworks often comes down to framework-specific optimization, and not all reference implementations or benchmark suite tests do what we need it to do out-of-the-box (not to mention third-party implementations). Analyzing the level of TF optimization is developer-level work, and that's beyond the scope of the article. But once benchmark suites hit their stride, that will resolve that issue for us.
For Keras, I wasn't able to find anything that was reasonably usable by a non-developer, though I could've easily missed something (I'm aware of how it relates to TF, Theano, MXNet, etc). I'm sure that if we replaced PyTorch with Tensorflow implementations, we would get questions on 'Where's PyTorch?' :)
Not to say your point isn't valid, it is :) We're going to keep on looking into it, rest assured.
SirPerro - Thursday, July 5, 2018 - link
Keras has some nice examples in its github repo to be run with the tensorflow backend but for the sake of benchmarking it does not offer anything that it's not covered by the pure tensorflow examples, I guessBurntMyBacon - Tuesday, July 3, 2018 - link
I believe the GTX Titan with memory clock 6Gbps and memory bus width of 384 bits should have a memory bandwidth of 288GB/sec rather than the list 228GB/sec. Putting that aside, this is a nice review.Nate Oh - Tuesday, July 3, 2018 - link
Thanks, fixedJon Tseng - Tuesday, July 3, 2018 - link
Don't be silly. All we care about is whether it can run Crysis at 8K.